Derivadas

HISTORIA:

Los problemas típicos que dieron origen al Cálculo Infinitesimal, comenzaron a plantearse en la época clásica de Grecia (siglo III a.C.), pero, no se encontraron métodos sistemáticos de resolución hasta 20 siglos después (en el siglo XVII por obra de Newton y Leibnitz).  

En lo que atañe a las derivadas, existen dos conceptos de tipo geométrico: el problema de la tangente a una curva (concepto griego estático en contraste con el concepto cinemático de Arquímedes) y el problema de los extremos (máximos y mínimos) que en su conjunto dieron origen a lo que modernamente se conoce como Cálculo Diferencial.  

El problema de la tangente a una curva, fue analizado y resuelto primeramente por Apolonio (200 a.C.). En el libro II de su obra, hace el estudio de los diámetros conjugados y de las tangentes a una cónica. Por ejemplo, si P es un punto cualquiera de una hipérbola de centro C, entonces, Apolonio demuestra que la tangente en P corta las asíntotas en los puntos L y L’ que equidistan de P. 

TASA DE VARIACIÓN MEDIA Y INSTANTÁNEA;
-Tasa de variación media:
Se define tasa de variación media de la función f en un intervalo [a,b] del dominio de f(x) al cociente:

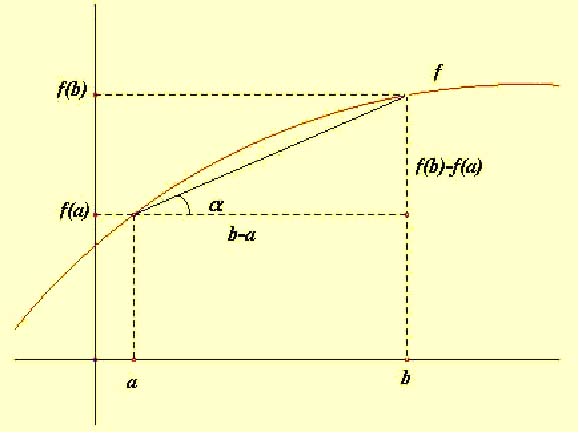
Ejemplo:

-Tasa de variación instantánea:

Ese número de la tasa de variación instantánea de la función f en el punto 

si escribimos 

    

Ejemplo:

Derivada de una función en un punto

Se define la derivada de la función f en un punto p de la abcisa como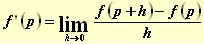   

cuando este límite exista y además sea finito.

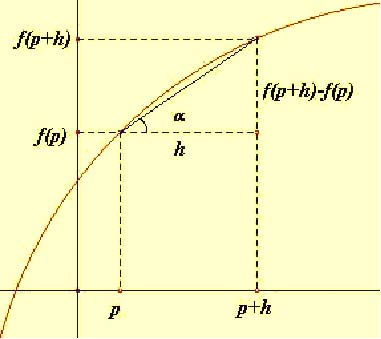
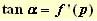
DERIVADAS DE FUNCIONES ELEMENTALES 

Función	Derivada	Ejemplos
Constante
y=k	y'=0	y=8	y'=0
Identidad
y=x	y'=1	y=x	y'=1
Funciones potenciales
Funciones exponenciales
Funciones logarítmicas
Funciones trigonométricas
Derivadas de sumas, restas, productos y cocientes de funciones

APLICACIONES DE LA DERIVADA:

• Recta tangente a una función en un punto.

Si f(x) es una función, entonces en x = a  f(a) es la pendiente de la recta tangente a f(x) para a.

En la figura se muestra la gráfica de y =-x² +4x, una recta secante que pasa por el punto (1, 3) y la recta tangente en ese punto, que tiene por ecuación

 y –3 = 2(x-1)

• Representación de gráficas.

El conocimiento de una función se completa perfectamente dibujando su gráfica, los siguientes resultados dan una idea aproximada de ésta:

I) Estudio de f 

1º Dominio de f.

2º Puntos de corte con los ejes.

3º Signo de la función (regiones en las que varía el signo).

4º Simetrías.

- Si f(-x) = f(x), función par, simétricas respecto del eje de ordenadas.

- Si f(-x) =-f(x), función impar, simétrica respecto del origen.

5º Asíntotas

- Verticales

Si existe a tal que , x =a es la ecuación de una asíntota vertical.

- Horizontales

Si ,  y =b es una asíntota horizontal.

- Oblicuas

Si    y  , y =m x +n es una asuntota oblicua.

II) Estudio de f’ 

1º Crecimiento y decrecimiento.

Si f ’(x)>0 , f es creciente. Si f ’(x)<0, f es decreciente.

2º Máximos y mínimos relativos

Condición necesaria de máximo y mínimo es que f ’(x)=0.

III) Estudio de f’’

1º Concavidad y convexidad, f ’’>0 convexa È, f ’’<0 cóncava.

2º S i f ’’(x₀) =0 y en dicho punto cambia la curvatura es punto de inflexión.

EJEMPLO:

• Problemas de optimización.

Pasos para la resolución de problemas de optimización

1. Se plantea la función que hay que maximizar o minimizar.
2. Se plantea una ecuación que relacione las distintas variables del problema, en el caso de que haya más de una variable.
3. Se despeja una variable de la ecuación y se sustituye en la función de modo que nos quede una sola variable.
4. Se deriva la función y se iguala a cero, para hallar los extremos locales.
5. Se realiza la 2ª derivada para comprobar el resultado obtenido.