1.1.Historia de los números reales:

Los egipcios utilizaron por primera vez las fracciones comunes alrededor del año 1000 a. C.; alrededor del 500 a. C. un grupo de matemáticos griegos liderados por Pitágoras se dio cuenta de la necesidad de los números irracionales. Los números negativos fueron ideados por matemáticos indios cerca del 600, posiblemente reinventados en China poco después, pero no se utilizaron en Europa hasta el siglo XVII, si bien a finales del XVIII Leonhard Euler descartó las soluciones negativas de las ecuaciones porque las consideraba irreales. En ese siglo, en el cálculo se utilizaba un conjunto de números reales sin una definición concisa, cosa que finalmente sucedió con la definición rigurosa hecha por Georg Cantor en 1871.
En realidad, el estudio riguroso de la construcción total de los números reales exige tener amplios antecedentes de teoría de conjuntos y lógica matemática. Fue lograda la construcción y sistematización de los números reales en el siglo XIX por dos grandes matemáticos europeos utilizando vías distintas: la teoría de conjuntos de Georg Cantor (encajamientos sucesivos, cardinales finitos e infinitos), por un lado, y el análisis matemático de Richard Dedekind (vecindades, entornos y cortaduras de Dedekind). Ambos matemáticos lograron la sistematización de los números reales en la historia, no de manera espontánea, sino utilizando todos los avances previos en la materia: desde la antigua Grecia y pasando por matemáticos como Descartes, Newton, Leibniz, Euler,Lagrange, Gauss, Riemann, Cauchy y Weierstrass.
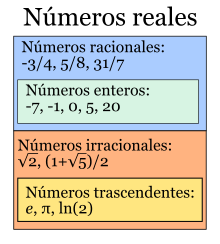
El conjunto formado por los números racionales e irracionales es el conjunto de los números reales, se designa por  .
.

Con los números reales podemos realizar todas las operaciones, excepto la radicación de índice par y radicando negativo, y la división por cero.
1.2.Números racionales:
En matemática, se llama número racional a todo número que puede representarse como el cociente de dos números enteros, es decir, una fracción común a/b con numerador a y denominador distinto de cero b. El término racional alude a fracción o parte de un todo. El conjunto de los números racionales se denota por Q que deriva de «cociente» (Quotient en varios idiomas europeos). Este conjunto de números incluye a los números enteros ( ), y es un subconjunto de los números reales (
), y es un subconjunto de los números reales ( ).
).
 ), y es un subconjunto de los números reales (
), y es un subconjunto de los números reales ( ).
).
La escritura decimal de un número racional es, o bien un número decimal finito, o bien periódico. Esto es cierto no solo para números escritos en base 10 (sistema decimal), también lo es en base binaria, hexadecimal o cualquier otra base entera. Recíprocamente, todo número que admite una expansión finita o periódica (en cualquier base entera), es un número racional.
Un número real que no es racional, se llama número irracional; la expansión decimal de los números irracionales, a diferencia de los racionales, es infinita no-periódica.
En sentido estricto, número racional es el conjunto de todas las fracciones equivalentes a una dada; de todas ellas, se toma comorepresentante canónico de dicho número racional a la fracción irreducible. Las fracciones equivalentes entre sí –número racional– son unaclase de equivalencia, resultado de la aplicación de una relación de equivalencia sobre  .
.
 .
.
1.3.La recta real:
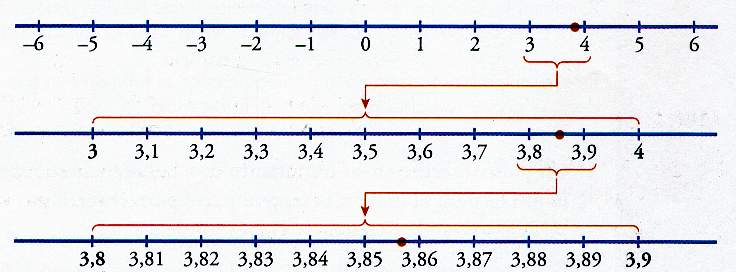
La recta numérica real o recta de coordenadas es una representación geométrica del conjunto de los números reales. Tiene su origen en el cero, y se extiende en ambas direcciones, los positivos en un sentido (normalmente hacia la derecha) y los negativos en el otro (normalmente a la izquierda). Existe una correspondencia uno a uno entre cada punto de la recta y un número real.
1.4.Intervalos y entornos:
Intervalos:
un intervalo es un conjunto comprendido entre dos valores. Específicamente, un intervalo real es un subconjunto conexo de la recta real, es decir, una porción de recta entre dos valores dados.

El conjunto [a,b] se llama intervalo cerrado y (a,b) se llama intervalo abierto. En cualquiera de los casos b-a se llama longitud del intervalo.
Entornos:
Se llama entorno de centro a y radio r, y se denota por Er(a) o E(a,r), al intervalo abierto (a-r, a+r).
Er(a) = (a-r, a+r)

Los entornos se expresan con ayuda del valor absoluto.
Er(0) = (-r, r) se expresa también |x|<r, o bien, -r < x < r.
Er(a) = (a-r, a+r) se expresa también |x-a|<r, o bien, a a-r < x < a+r.
1.5.Radicales:
Un radical es una expresión de la forma  , en la que n
, en la que n 
 y a
y a 
 ; con tal que cuando a sea negativo, n ha de ser impar.
; con tal que cuando a sea negativo, n ha de ser impar.

1.6 Números combinatorios, binomio de newton:

Propiedades de los números combinatorios:
1.
2.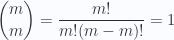
3.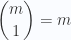
4.Números combinatorios complementarios: 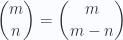
5.Formula de Stifel: 
Con estás propiedades y lo que sabemos de expresiones factoriales podemos construir el triángulo de Tartaglia (Pascal) y resolver ya ecuaciones con números combinatorios


1.7.Logaritmos:
El logaritmo de un número, en una base dada, es el exponente al cual se debe elevar la base para obtener el número.

Propiedades de los logaritmos:
No existe el logaritmo de un número con base negativa.
No existe el logaritmo de un número negativo.
No existe el logaritmo de cero.
El logaritmo en base a de una potencia en base a es igual al exponente.
Operaciones con logaritmos:
Logaritmo de una multiplicación
El logaritmo de una multiplicación es igual a la suma de los logaritmos de los factores.
Logaritmo de una división
El logaritmo de un cociente es igual al logaritmo del dividendo menos el logaritmo del divisor.

Logaritmo de una potencia
El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base.
Logaritmo de una raíz
El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz.
Cambio de base
No hay comentarios:
Publicar un comentario