Trigonometría

Relaciones entre las razones trigonométricas 

Sería deseable conocer todas la posibles relaciones entre las distintas razones trigonométricas con el fin de poder dedudir unas a partir de otras. Con las relaciones que vamos a establecer se obtendrán todas las razones de un ángulo a partir de una dada.
De las definiciones se deduce que:

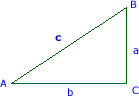Consideremos el senA = a/c y el cosA = b/c, si sumamos sus cuadrados y tenemos en cuenta el teorema de Pitágoras a²+b² = c²

se obtine la relacion fundamental de trigonometría 
sen²A + cos² A = 1 
Si dividimos los dos miembros de la igualdad por cos² A se obtiene una segunda igualdad 
1 + tg² A = sec²A
Si dividimos los dos miembros de la igualdad por sen² A se obtiene una segunda igualdad 
1 + cotg² A = cosec²A

A partir de las relaciones anteriores se pueden obtener todas las relaciones trigonométricas conocida una y el cuadrante en el que se encuentra, recordemos el signo del seno y el coseno dependiendo del cuadrante donde se encuentre el ángulo.

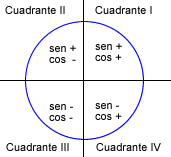
Razones trigonométricas de la suma y la diferencia de ángulos

Transformación de sumas en productos

Resumiendo:

sen A+sen B = 2 sen

A+B 2

cos

A-B 2

sen A-sen B = 2 sen

A-B 2

cos

A+B 2

cosA+cosB = 2 cos

A+B 2

cos

A-B 2

cosA-cosB = -2 sen

A+B 2

sen

A-B 2

 

Razones trigonométricas del ángulo doble y del ángulo mitad

Ya aprendimos que

Hagamos , con lo que obtendremos que:

 o sea   

De forma análoga podemos determinar que:

Para determinar las funciones trigonométricas del ángulo mitad, hagamos 

Sabemos que: 

 reemplazando  obtenemos:                                          

despejando:

                        

consideramos ahora que: 

                                             

                                      

Entonces:

despejando

Por último, ya que las otras se pueden determinar mediante la identidad

remplazando  obtenemos 

 o sea 

         Ecuaciones y sistemas de ecuaciones trigonométricas 

Ecuaciones trigonométricas: 

Una ecuación trigonométrica es aquella en la que la incógnita aparece como argumento en una o varias razones trigonométricas. 

Ejemplo:

Sistemas de ecuaciones trigonométricas:

Para resolver sistemas de ecuaciones trigonométricas se utilizan los habituales  métodos de sustitución o de reducción.

Ejemplo:

     este sistema lo vamos a resolver mediante el método de sustitución

               

            

Teorema del seno y del coseno

Teorema del seno:

En cualquiera triángulo ABC se verifica que: 

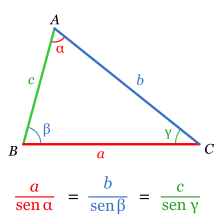
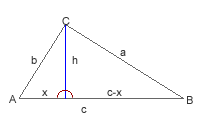
Teorema del coseno:

En cualquiera triangulo ABC se verifica que: 

                                                                     

Resolución de triángulos

Conocemos un lado y dos ángulos:

Sabiendo que la suma de los tres ángulos es 180º, calculamos el tercer ángulo y mediante el teorema del seno calculamos los otros dos lados.

Conocemos dos lados y el ángulo opuesto a uno de ellos:

Aplicamos el teorema del seno para obtener el ángulo que es opuesto a uno de los lados dados y aplicamos nuevamente el teorema de los senos.