Historia y definición de los vectores
En física, matemáticas e ingeniería, un vector (también llamado vector euclidiano o vector geométrico) es una herramienta geométrica utilizada para representar una magnitud física definida por un módulo (o longitud) y una dirección (u orientación).
Los vectores se pueden representar geométricamente como segmentos de recta dirigidos o flechas en el plano 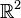 o en el espacio
o en el espacio  .
.
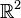 o en el espacio
o en el espacio  .
.
Un vector fijo  es un segmento orientado que va del punto A (origen) al punto B (extremo).
es un segmento orientado que va del punto A (origen) al punto B (extremo).
Módulo, dirección y sentido del vector fijo 
Módulo:
Es la longitud o tamaño del vector. Para hallarla es preciso conocer el origen y el extremo del vector, pues para saber cuál es el módulo del vector, debemos medir desde su origen hasta su extremo.
Dirección:
Viene dada por la orientación en el espacio de la recta que lo contiene.
Sentido:
Se indica mediante una punta de flecha situada en el extremo del vector, indicando hacia qué lado de la línea de acción se dirige el vector.
Vectores equipolentes:Dos vectores son equipolentes cuando tienen igual módulo, dirección y sentido.

Vectores libres en 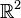
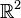
El conjunto de todos los vectores equipolentes entre sí se llama vector libre. Es decir los vectores libres tienen el mismo módulo, dirección y sentido.
Módulo, dirección y sentido del vector libre
Se llama módulo, dirección y sentido de un vector libre no nulo, al módulo, dirección y sentido de uno cualquiera de sus representantes.
Operaciones con vectores. Dependencia lineal
Suma y resta de vectores libres:
La suma de dos vectores libres es otro vector libre que se determina de la siguiente forma:
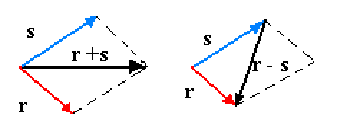
Se sitúa el punto de aplicación de uno de ellos sobre el extremo del otro; el vector suma es el vector que tiene su origen en el origen del primero y su extremo en el extremo del segundo.
Por tanto, el vector suma de dos vectores coincide con una de las diagonales, la "saliente", del paralelogramo que puede formarse con los vectores que se suman; la otra diagonal representa la resta de dichos vectores.
Se sitúa el punto de aplicación de uno de ellos sobre el extremo del otro; el vector suma es el vector que tiene su origen en el origen del primero y su extremo en el extremo del segundo.
Por tanto, el vector suma de dos vectores coincide con una de las diagonales, la "saliente", del paralelogramo que puede formarse con los vectores que se suman; la otra diagonal representa la resta de dichos vectores.
Base canónica
Los vectores  =(1,0) y
=(1,0) y  = (0,1) reciben el nombre de base canónica de los vectores del plano, y los escalares u1 y u2, componentes de
= (0,1) reciben el nombre de base canónica de los vectores del plano, y los escalares u1 y u2, componentes de  =(u1,u2) en la base canónica.
=(u1,u2) en la base canónica.

Operaciones de vectores con coordenadas
Suma y resta de vectores libres:
La suma y resta de vectores se realiza sumando o restando cada una de las componentes de cada uno y da como resultado otro vector.
V1 = (x1, y1)
V2 = (x2, y2)
V1 + V2 = (x1, y1) + (x2, y2) = (x1 + x2, y1+ y2)
Gráficamente la suma y resta de vectores se puede realizar por el método del paralelogramo, es decir trazar sobre cada vector una recta paralela al otro formando un paralelogramo, cuya diagonal es la suma.
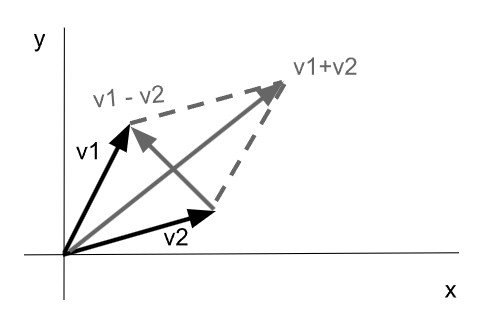
Modulo y argumento de un vector:
Modulo:
Aplicando el teorema de Pitágoras, tomando la longitud de cada cateto como el valor de cada coordenada del vector, obtenemos la longitud del segmento a la que llamamos módulo del vector.
El módulo del vector nos sirve también para calcular la distancia entre dos puntos que han servido de origen y extremo, es decir, distancia(P,Q) = PQ = módulo(v).
Argumento:
La dirección de un vector viene señalada por la recta que lo contiene y todas sus paralelas, o lo que es lo mismo, por el ángulo que forma con la horizontal (argumento). Fíjate que puedes aplicar la definición de tangente trigonométrica para calcular el argumento, es decir si v(vx,vy) tiene por argumento α ocurrirá que tg α=vy/vx , de lo que obtenemos dos valores para α (en dos cuadrantes diferentes) que nos marcarán la misma dirección pero sentidos contrarios. El vector v está perfectamente definido por su módulo R y el argumento α, así v=Rα definirá el vector y se llaman coordenadas polares.
Producto escalar de dos vectores
El producto escalar de dos vectores, expresado analíticamente como r · v, se obtiene de la suma de los productos formados por las componentes de uno y otro vector. Es decir, dados dos vectores r y v, expresados en un mismo sistema de coordenadas:
teniendo en cuenta que el producto escalar de los vectores :
Esta operación no solo nos permite el cálculo de la longitud de los segmentos orientados que representan ( sus módulos ), sino también calcular el ángulo que hay entre ellos. Esto es posible, ya que el producto escalar también se puede hallar en función de sus módulos y del coseno del ángulo que forman mediante la fórmula :
El producto escalar de dos vectores es por definición un escalar.
Con lo que deducimos que:
r = rxi + ryj + rzk
v = vxi + vyj + vzk
i · i = j · j = k · k = 1
i · j = i · k = j · k = 0
el resultado de multiplicar escalarmente r por v es:
r · v = |r| · |v| · cos (r, v)
El producto escalar de dos vectores es igual al módulo de uno de ellos por la proyección del otro sobre el primer.
Ángulo de dos vectores:
Con lo que deducimos que:
Y dónde esta la HISTORIA?
ResponderEliminarx2
Eliminarx3
EliminarX3
ResponderEliminarx4
ResponderEliminarX5
ResponderEliminarx6
ResponderEliminarY la historia de donde provienen los vectores
ResponderEliminarx7
ResponderEliminarx8
ResponderEliminarx9
ResponderEliminar