sábado, 21 de enero de 2012

Trigonometría

HISTORIA


La trigonometría es una rama de la matemática, cuyo significado etimológico es "la medición de los triángulos". Deriva de los términos griegos τριγωνοtrigōno triángulo y μετρον metron medida.
Los antiguos egipcios y los babilonios conocían ya los teoremas sobre las proporciones de los lados de los triángulos semejantes. Pero las sociedades pre-helénica carecían de la noción de una medida del ángulo y por lo tanto, los lados de los triángulos se estudiaron en su medida, un campo que se podría llamar "trilaterometría".
Los astrónomos babilonios llevaron registros detallados sobre la salida y puesta de las estrellas, el movimiento de los planetas y los eclipses solares y lunares, todo lo cual requiere la familiaridad con la distancia angular medida sobre la esfera celeste. Sobre la base de una interpretación de la tablilla cuneiforme Plimpton 322 (c. 1900 aC), algunos incluso han afirmado que los antiguos babilonios tenían una tabla de secantes. Hoy, sin embargo, hay un gran debate acerca de si se trata de una tabla de ternas pitagóricas, una tabla de soluciones de ecuaciones segundo grado, o una tabla trigonométrica.                                 


Tablilla babilonia Plimpton 322.

Papiro de Ahmes
Los egipcios, en el segundo milenio antes de Cristo, utilizaban una forma primitiva de la trigonometría, para la construcción de las pirámides. El Papiro de Ahmes, escrito por el escriba egipcio Ahmes (c. 1680-1620 aC), contiene el siguiente problema relacionado con la trigonometría:
"Si una pirámide es de 250 codos de alto y al lado de su base de 360 codos de largo, ¿cuál es su Seked?"
La solución, al problema, es la relación entre la mitad del lado de la base de la pirámide a su altura. En otras palabras, la cantidad que encontró para laseked es la cotangente del ángulo que forman la base de la pirámide y su cara.






                    Media de ángulo. el radián

El radián es la unidad de ángulo plano en el Sistema Internacional de Unidades. Representa el ángulo central en una circunferencia y abarca un arco cuya longitud es igual a la del radio. Su símbolo es rad.
Relaciones entre grados sexagesimales y radianes:
Se parte de la base de que una circunferencia completa tiene 2π radianes, y que una circunferencia tiene 360° sexagesimales, luego tenemos:
\rm {360} \; {grados} = {2\pi} \; {radianes}
\rm {180} \; {grados} = {\pi} \; {radianes}
Razones trigonométricas de un ángulo agudo

Llamamos razones trigonométricas a las distintas razones existentes entre los lados de un triángulo rectángulo. Se define:
Seno de un ángulo como la razón entre el cateto opuesto al ángulo y la hipotenusa.
Coseno de un ángulo como la razón entre el cateto contiguo al ángulo y la hipotenusa.
Tangente de un ángulo como la razón entre el cateto opuesto y el contiguo.
Cosecante de un ángulo como la razón entre la hipotenusa y el cateto opuesto, de ahí se deduce que la consecante es 1 entre el seno
Secante de un ángulo como la razón entre la hipotenusa y el cateto contiguo, es 1 entre el coseno.
Cotangente de un ángulo es la razón entre el cateto contiguo y el cateto opuesto, es 1 entre la tangente.


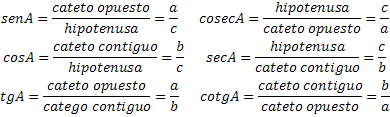
Razones trigonométricas
De las definiciones anteriores se deduce que:




Razones trigonométricas de un ángulo cualquiera
        


       Si situamos los ángulos sobre la circunferencia goniométrica obtenemos:
  • La proyección del segundo lado sobre el eje de las x, considerada con signo, nos dará el Coseno.  
  • La proyección del segundo lado sobre el eje de las y, considerada con signo, nos dará el Seno.
  • El cociente entre Seno y Coseno, nos dará la Tangente. Obviamente, cuando el Coseno del ángulo valga 0, la Tangente no estará definida.

Razones Trigonométricas










Con esta ampliación de las definiciones para el Seno, Coseno y Tangente de un ángulo cualquiera podemos observar que:
  1. El Seno de un ángulo cualquiera tiene que valer necesariamente entre -1 y 1
  2. Sen(0º)=0, Sen(90º)=1, Sen(180º)=0 y Sen(270º)=-1
  3. El Coseno de un ángulo cualquiera tiene que valer entre -1 y 1
  4. Cos(0º)=1, Cos(90º)=0, Sen(180º)=-1 y Sen(270º)=0
  5. La Tangente de un ángulo puede tomar cualquier valor entre +∞ y -∞
  6. Tag(90º) y Tag(270º) no están definidas pues son un cociente entre 0.

Razones trigonométricas en los cuadrantes segundo, tercero y cuarto

Vamos a partir de la circunferencia de centro (0,0) y radio1. Trazamos ahora un ángulo A. El segmento que parte del (0,0) y determina dicho ángulo corta a la circunferencia en el punto P. Trazamos ahora las dos perpendiculares a los ejes desde este punto P, que cortan en los puntos Q y R en los ejes X,Yrespectivamente. En esta situación, el coseno de este ángulo A es la longitud del segmento del eje X que va del (0,0) hasta Q (en la imagen, el segmento azul) y el seno de A es la longitud del segmento del eje Y que va del (0,0) hasta R (en la imagen, el segmento rojo). Esto es, el coseno se mide en el eje X y el seno se mide en el eje Y.
La idea para calcular las razones trigonométricas de un ángulo de un cuadrante que no sea el primer es asociar ese ángulo con el ángulo simétrico a él del primer cuadrante, teniendo cuidado con los signos.
Comencemos con los signos. Hay una regla muy sencilla para aprenderse los signos de seno, coseno y tangente en cada uno de los cuadrantes. Se basa en la frase:
TODAS SIN TACOS
Y se desglosa de la siguiente forma:
- En el primer cuadrante todas son positivas.
- En el segundo cuadrante sólo es positivo el seno (sin en inglés).
- En el tercer cuadrante sólo es positiva la tangente.
- En el cuarto cuadrante sólo es positivo el coseno.
Y ahora vamos con el tema de los ángulos simétricos:
  • Segundo cuadrante
    El ángulo del primer cuadrante simétrico a uno del segundo cuadrante es el que queda en el primer cuadrante al doblar el dibujo por el eje Y. Por ejemplo, el simétrico de \textstyle{\frac{3 \pi}{4}}en el primer cuadrante es \textstyle{\frac{\pi}{4}}. Entonces las razones trigonométricas de un ángulo del segundo cuadrante tienen el mismo valor que las correspondientes a su ángulo simétrico del primero (que podemos calcular con la tabla) pero añadiendo un signo menos a los valores del coseno y la tangente. La situación descrita podéis verla en esta imagen:
    Veamos ahora un ejemplo numérico con el ángulo 120^\circ=\textstyle{\frac{2 \pi}{3}}. El simétrico de \textstyle{\frac{2 \pi}{3}} en el primer cuadrante es 60^\circ=\textstyle{\frac{\pi}{3}} (esto es fácil de ver con el truco de doblar el dibujo por el eje Y). Entonces:
    • sen \left (\frac{2 \pi}{3} \right )= sen \left (\frac{\pi}{3} \right )=\frac{\sqrt{3}}{2}
    • cos \left (\frac{2 \pi}{3} \right )= -cos \left (\frac{\pi}{3} \right )=-\frac{1}{2}
    • tg \left (\frac{2 \pi}{3} \right )= -tg \left (\frac{\pi}{3} \right )=-\sqrt{3}
  • Tercer cuadrante
    Para este caso la base es la misma que en el anterior. El simétrico de un ángulo del tercer cuadrante en el primero es el ángulo que queda en este primer cuadrante aldoblar el dibujo por el eje X y luego por el eje Y. En este caso la razones trigonométricas de este ángulo tienen el mismo valor que las de su simétrico en el primer cuadrante (tabla) pero añadiendo un signo menos a los valores del seno y del coseno. Lo podéis ver en la siguiente imagen:
    Por ejemplo, para 225^\circ=\textstyle{\frac{5 \pi}{4}}, cuyo simétrico es \textstyle{\frac{\pi}{4}}, tenemos lo siguiente:
    • sen \left (\frac{5 \pi}{4} \right )= -sen \left (\frac{\pi}{4} \right )=-\frac{\sqrt{2}}{2}
    • cos \left (\frac{5 \pi}{4} \right )= -cos \left (\frac{\pi}{4} \right )=-\frac{\sqrt{2}}{2}
    • tg \left (\frac{5 \pi}{4} \right )= tg \left (\frac{\pi}{4} \right )=1
  • Cuarto cuadrante
    En este caso la situación vuelve a ser muy similar. El simétrico de un ángulo de este cuadrante en el primero se obtiene doblando el dibujo por el eje X. Por ello la razones trigonométricas de un ángulo del cuarto cuadrante tienen el mismo valor que las de su simétrico en el primer cuadrante (tabla) pero añadiendo un signo menos a los valores del seno y de la tangente. En esta imagen puede observarse dicha situación:
    Y ahora un ejemplo numérico, esta vez con 330^\circ=\textstyle{\frac{11 \pi}{6}}, cuyo simétrico en el primer cuadrante es \textstyle{\frac{\pi}{6}}:
    • sen \left (\frac{11 \pi}{6} \right )= -sen \left (\frac{\pi}{6} \right )=-\frac{1}{2}
    • cos \left (\frac{11 \pi}{6} \right )= cos \left (\frac{\pi}{6} \right )=\frac{\sqrt{3}}{2}
    • tg \left (\frac{11 \pi}{6} \right )= -tg \left (\frac{\pi}{6} \right )=-\frac{1}{\sqrt{3}}








Publicado por en

3 comentarios:

Suscribirse a: Enviar comentarios (Atom)